摘要:采用可壓縮流體的高階有限容積法(FVM)及其系列改進算法對燃氣管道進行了穩態分析,探討了數學模型的建立和數學模型的求解。通過實例對比可知,FVM方法具有較快的運算速度和較好的收斂性,計算結果較準確。
關鍵詞:燃氣管道;穩態分析;水力計算;有限容積法
Steady-state Simulation and Analysis of Gas Pipeline Based on Finite Volume Method
LIU Xiaojing,ZHOU Weiguo,WANG Hai
Abstract:The steady-state analysis of gas pipeline is conducted using compressible fluid high-order finite volume method(FVM)and its improved algorithms.The establishment and solution of mathe-matical model are discussed.The ease comparison shows that FVM has rapider operation speed,better convergence and exact calculation result.
Key words:gas pipeline;steady-state analysis;hydraulic calculation;finite volume method(FVM)
1 概述
天然氣管網穩態分析是天然氣管網設計和改造的依據,是進行管網動態模擬和分析的基礎,也是加強天然氣管網系統優化運行以及確定最優改擴建方案的基礎。管道模擬準確與否關鍵在于所建立的數學模型能否準確、全面地描述管內流動過程以及能否找到快速求解模型且收斂性好的方法。
在HARDY等人提出迭代法解非線性方程后,目前常用的穩態分析方法有牛頓-拉夫遜(Newton-Raphson)法、線性逼近法、流體網絡理論。管延文、段常貴等都曾用牛頓-拉夫遜法進行過計算[1~2]。牛頓-拉夫遜法是求解天然氣管網穩態分析節點法數學模型的常用算法,但它有兩個主要缺點:①每次迭代都要計算雅可比矩陣及其逆矩陣,計算量大;②對迭代初始值要求比較高,如不能提供較好的初始值,則收斂較慢,甚至計算過程發散[3]。國內的姜東琪等[4]和國外的KE[5]也采用線性逼近法對燃氣管網進行過水力計算。KE和TA0等人利用流體網絡理論對管網進行了穩態模擬[6~7]。西南石油大學對燃氣管網的穩態計算方法進行了研究,分別應用節點法和環路法進行求解,但在計算中忽略了壓縮因子對氣體流動的影響[8]。進行管網水力計算時,必須考慮管道中燃氣的可壓縮性。
本文采用SIMPLE改進算法,用有限容積法(FVM)導出的離散方程可以保證具有守恒特性,而且離散方程系數的物理意義明確。這克服了采用有限差分法求解管網流動偏微分方程的多種困難;也可以克服管網計算中各管段管徑不同,以及在連接處流量突變的困難。對不同的管段進行長度不同的離散容積劃分,不會影響計算結果的連續性和迭代的收斂穩定性。而傳統方法離散時,為了保證計算結果收斂,必須對長管段進行很細密的網格劃分,導致計算時間很長且無法保證數值解的守恒性。根據有限容積法離散方程的特點,可以采用高效的TDMA算法,存儲量很小[9]。
2 數學模型的建立
① 管道數學模型
管道內氣體流動數學模型由動量方程、連續性方程、狀態方程組成[10],見式(1)。因為管道內溫度變化很小,所以不考慮能量方程。
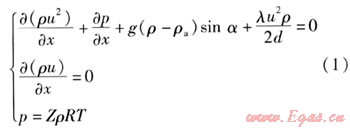
式中ρ——燃氣密度,kg/m3
u——燃氣速度,m/s
x——管道軸向坐標,m
p——燃氣壓力,Pa
g——重力加速度,m/s2
ρa——空氣密度,kg/m3
α——管道與水平面夾角,rad
λ——管道摩擦阻力系數
d——管道內徑,m
z——壓縮因子
R——氣體常數,J/(kg·K)
T——燃氣溫度,K
② 模型的簡化
a. 在動量方程中,對流項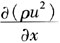 只在燃氣流速極大(接近聲速)時才有意義,而通常管道中燃氣流速不大于40m/s。此外,在高壓管網瞬態變化中,對流項
只在燃氣流速極大(接近聲速)時才有意義,而通常管道中燃氣流速不大于40m/s。此外,在高壓管網瞬態變化中,對流項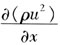 相對于其他項數值較小,可以忽略[11]。b.在城市燃氣管網中,管道的標高差值不太大,因此,動量方程中的重力項g(ρ-ρa)sinα一般忽略不計。
相對于其他項數值較小,可以忽略[11]。b.在城市燃氣管網中,管道的標高差值不太大,因此,動量方程中的重力項g(ρ-ρa)sinα一般忽略不計。
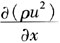 只在燃氣流速極大(接近聲速)時才有意義,而通常管道中燃氣流速不大于40m/s。此外,在高壓管網瞬態變化中,對流項
只在燃氣流速極大(接近聲速)時才有意義,而通常管道中燃氣流速不大于40m/s。此外,在高壓管網瞬態變化中,對流項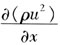 相對于其他項數值較小,可以忽略[11]。b.在城市燃氣管網中,管道的標高差值不太大,因此,動量方程中的重力項g(ρ-ρa)sinα一般忽略不計。
相對于其他項數值較小,可以忽略[11]。b.在城市燃氣管網中,管道的標高差值不太大,因此,動量方程中的重力項g(ρ-ρa)sinα一般忽略不計。 通過簡化,可以得到仿真數學模型,見式(2)。

式中C——常量
③ 摩擦阻力系數
管道摩擦阻力系數除與燃氣性質、管道材質等因素有關外,還與燃氣的流動狀態有關。不分低壓和高中壓管道,統一按流動狀態和管道材質來分類選取計算公式,進行燃氣管道摩擦阻力系數的計算[12]。
3 數學模型的求解
① 數學模型的求解
在計算氣體穩定流動時,利用有限容積法一維交錯網格將壓力-速度耦合方程中不同的變量離散式存儲在不同的網格系統,將式(2)中的動量方程進行離散,見式(3)。i節點是速度控制容積的中心節點,I節點是壓力控制容積的中心節點。
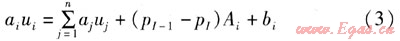
式中ai——i節點的離散方程系數,kg/s
ui——i節點的速度,m/s
n——i節點周圍的節點數
aj——i節點周圍各節點的離散方程系數,kg/s
uj——i節點周圍各節點的速度,m/s
pI-1——I-1節點的壓力,Pa
pI——I節點的壓力,Pa
Ai——速度控制容積的界面面積,m2
bi——方程源項,(kg·m)/s2
在初始壓力下:
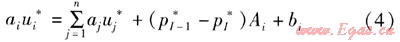
式中ui*——初始壓力下i節點的速度,m/s
uj*——初始壓力下,i節點周圍各節點的速度,m/s
pI-1*——I-1節點的初始壓力,Pa
pI*——I節點的初始壓力,Pa
設修正的壓力方程為:
p=p*+p′ (5)
式中p′——壓力修正值,Pa
設修正的速度方程為:
u=u*++u′ (6)
式中u′——速度修正值,m/s
由式(4)~(6)得:

式中ui′——i節點速度修正值,m/s
uj′——i節點周圍各節點速度修正值,m/s
pI-1′——I-1節點的壓力修正值,Pa
pI′——I節點的壓力修正值,Pa
由于式(7)第一項是周圍節點速度引起的修正值,值很小;而第二項是同一方向相鄰節點壓力差引起的修正值,影響較大。故為簡化計算,略去第一項,并由式(6)、(7)得到速度的改進值:
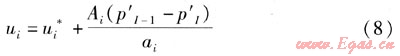
將速度改進值代入方程組(2)的連續性方程中,并將壓力修正值p′的系數歸一化處理,得到壓力修正方程:
aIpI′=aI+1pI+1′+aI-1pI-1′+bI′ (9)
式中aI——I節點離散方程系數,kg/m
aI+1——I+1節點離散方程系數,kg/m
pI+1′——I+1節點的壓力修正值,Pa
aI-1——I-1節點離散方程系數,kg/m
bI′——由于速度場的不正確引起的不平衡量,kg/s
經過多次迭代修正,最終bI′是否趨于0可以作為判斷迭代過程是否滿足要求的判據。
在計算時,管道內氣體壓力和流速的分布采用雙精度Simple方法的PIS0模型進行求解。即通過壓力預測一修正方法,包括1個預測步驟和2個校正步驟,不斷地修正計算結果,反復迭代,最后求出壓力和速度的收斂解。
② 程序編制
采用VB編寫計算程序,對網格參數、壓力參數內循環迭代的計算均采用穩定且快速收斂的TDMA方法。
4 實際應用與分析
為驗證燃氣管網仿真軟件是否準確,英國氣體公司倫敦研究站(LRS)采用了一組不同管徑、流量下符合實際的燃氣的穩態數據進行驗證。在相同的管徑、流量條件下,本文采用FVM方法進行穩態仿真,并將仿真結果與新加坡國立大學采用電網絡傳輸線理論的模擬結果進行對比。
p1,p2,p3,p4,p5分別表示管道被平均分為4段后,5個節點處的壓力值。FVM方法的仿真結果與LRS的數據對比見表1,新加坡國立大學的電網絡傳輸線理論模擬結果與LRS的數據對比見表2。
表1 FVM方法仿真結果與LRS數據對比
|
管道長度/km
|
管道內徑/m
|
流量/(m3·s-1)
|
相對誤差/%
|
||||
|
p1
|
p2
|
p3
|
p4
|
p5
|
|||
|
128.747
|
0.457
|
0.408
|
0.000
|
0.057
|
0.074
|
0.088
|
0.004
|
|
128.747
|
0.457
|
0.612
|
0.000
|
0.100
|
0.182
|
0.436
|
0.009
|
|
32.187
|
0.305
|
0.218
|
0.000
|
0.206
|
0.105
|
0.237
|
0.O01
|
|
32.187
|
0.305
|
0.327
|
0.000
|
0.355
|
0.960
|
2.175
|
0.045
|
|
9.656
|
0.356
|
0.082
|
0.000
|
0.072
|
0.109
|
0.166
|
0.000
|
|
9.656
|
0.356
|
0.122
|
0.000
|
0.123
|
0.387
|
1.069
|
0.000
|
|
4.828
|
0.356
|
0.022
|
0.000
|
0.000
|
0.117
|
0.322
|
0.000
|
|
4.828
|
0.356
|
0.033
|
0.000
|
0.059
|
0.220
|
0.388
|
0.000
|
|
0.805
|
0.102
|
0.001
|
0.000
|
0.000
|
0.152
|
0.000
|
0.000
|
|
0.805
|
0.102
|
0.002
|
0.000
|
0.153
|
0.000
|
0.196
|
0.000
|
表2 新加坡國立大學的電網絡傳輸線理論模擬結果與LRS的數據對比
|
管道長度/km
|
管道內徑/m
|
流量/(m3·s-1)
|
相對誤差/%
|
||||
|
p1
|
p2
|
p3
|
p4
|
p5
|
|||
|
128.747
|
0.457
|
0.408
|
0.000
|
0.000
|
0.180
|
0.250
|
0.170
|
|
128.747
|
0.457
|
0.612
|
0.000
|
0.060
|
0.130
|
0.040
|
0.170
|
|
32.187
|
0.305
|
0.218
|
0.000
|
0.410
|
0.560
|
0.940
|
0.720
|
|
32.187
|
0.305
|
0.327
|
0.000
|
0.380
|
0.890
|
1.510
|
0.300
|
|
9.656
|
0.356
|
0.082
|
0.000
|
0.850
|
1.360
|
2.450
|
3.210
|
|
9.656
|
0.356
|
0.122
|
0.000
|
1.830
|
3.280
|
4.170
|
3.460
|
|
4.828
|
0.356
|
0.022
|
0.000
|
0.000
|
0.590
|
0.650
|
1.870
|
|
4.828
|
0.356
|
0.033
|
0.000
|
0.600
|
1.470
|
1.940
|
0.290
|
|
0.805
|
0.102
|
0.001
|
0.000
|
0.000
|
0.000
|
0.580
|
0.610
|
|
0.805
|
0.102
|
0.002
|
0.000
|
0.000
|
0.620
|
0.710
|
1.640
|
由表1可知,運用FVM方法的仿真結果與LRS的數據非常接近,平均相對誤差小于1.000%。表1與表2對比可知,FVM方法的仿真結果更準確。采用FVM方法具有較快的運算速度和較好的收斂性,為管網的動態分析提供了基礎,可以滿足工程的需要,對于管網的設計和安全控制都有重要的參考作用。
參考文獻:
[1] 管延文,王永剛,李統強,等.牛頓管段方程法的燃氣管網穩態分析[J].煤氣與熱力,2006,26(6):10-12.
[2] 段常貴,徐彥峰,呂文哲,等.燃氣管網的穩態分析[J].煤氣與熱力,2000,20(2):95-97.
[3] 白建輝,汪玉春,郜峰,等.天然氣管網穩態分析綜合方法[J].油氣儲運,2009,28(2):37-39.
[4] 姜東琪,杜建梅,崔建華,等.燃氣管網水力計算及水力計算圖的繪制[J].煤氣與熱力,2001,21(5):453-455.
[5] KE S L.Transient analysis of pipeline network(master’s theses)[D].Singapore:National University of Singapore.1999:54-60.
[6] KE S L.TI H C.Transient analysis of isothermal gas flow in pipeline network[J].Chemical Engineering Journal,2000,76(2):169-177.
[7] TAO W Q,TI H C.Transient analysis of gas pipeline network[J].Chemical Engineering Journal,1998,69(3):47-52.
[8] 李長明.燃氣管網水力計算程序設計基礎[M].北京:煤炭工業出版社,1997:10-80.
[9] 李人憲.有限體積法基礎[M].北京:國防工業出版社,2001:81-83.
[10] OSIADACZ A J.Different transient models——limitations.advantages and disadvantages[C]∥.28th Annual Meeting PSIGs.San Francisco,California:Pipe]ine Simulation Interest Group,1996:1-26.
[11] 段常貴.燃氣輸配[M].3版.北京:中國建筑工業出版社,2001:87-88.
[12] 蔣祥龍.燃氣管道摩擦阻力計算的探討[J].煤氣與熱力,2004,24(1):37-40.
(本文作者:劉曉婧 周偉國 王海 同濟大學機械工程學院 上海 201804)
贊 賞 分享
您可以選擇一種方式贊助本站

支付寶轉賬贊助

微信轉賬贊助