摘 要

摘　要：低滲透油氣藏壓裂水平井以形成多裂縫來提高產量，但由于裂縫內流動壓力損失和裂縫段間干擾，導致氣體沿裂縫面非均勻流入。為了準確預測氣藏壓裂水平井的產量，基于瞬時點(

摘　要：低滲透油氣藏壓裂水平井以形成多裂縫來提高產量，但由于裂縫內流動壓力損失和裂縫段間干擾，導致氣體沿裂縫面非均勻流入。為了準確預測氣藏壓裂水平井的產量，基于瞬時點(線)匯函數和疊加原理，考慮氣藏壓裂水平井裂縫干擾、裂縫面產量非均勻流入以及裂縫內變質量流動，采用空間和時間離散技術，建立了氣藏壓裂水平井儲層滲流和裂縫內流動耦合的產量預測模型。應用結果表明：考慮裂縫無限導流會導致計算結果高于實際產量；而裂縫上均勻流入的假設使得計算結果低于實際產量；由于裂縫干擾，水平井筒兩端裂縫的產量高于中間裂縫；由于裂縫上的非均勻產量流入以及裂縫內的摩阻損失，裂縫上產量在水平井筒附近出現局部峰值；隨著時間增加，峰值降低并且產量從裂縫中間位置向兩端轉移；裂縫上產量分布受生產時間和裂縫導流能力的影響，生產時間越長，導流能力越大，裂縫上產量分布越均勻。將所建產量預測模型計算結果與實例井和傳統模型計算結果進行了對比，其吻合程度高、可靠性強。

關鍵詞：致密氣藏  壓裂水平井  點(線)匯函數  疊加原理  非均勻流入  非穩態產量  計算

Yield calculation of a fractured horizontal well with a non-uniform gas flow on fracture surface

Abstract：The productivity would be enhanced dramatically through fracturing horizontal wells in low permeability reservoirs．Due to gas flow pressure loss and inter-fracture interference，there exists a non uniform gas rate along fracture faces．In order to predict the flow capacity accurately，this paper applied the instantaneous point sink(congruence)function and the superposition principle，taking into account fracture interference，non uniform gas flow rate，and fracture inner variable mass flow to set a flow rate prediction model，which also considering the coupling effect of reservoir seepage flow and fracture inner flow．Conclusions were made as follows．First，if fractures are treated as infinite conductivity，the calculated productivity will be higher than that of the actHal vield．while if a uniform rate on fracture faces is assumed，the calculated result will be rather lower．Second，due to the fraeture interference，the flow rates from the fractures at two ends are higher than those from the middle fractures；and due to a non uniform flow on fracture faces and fracture inner friction loss，a flow rate peak appears in the fractures close to the wellbore．However．the peak decreases with time and the flow rate transfers from the middle to the ends．And finally，the flow rate distribution of fractures is affected by producing time and fracture conductivity，in particular，the flow rate distribution is becoming uniform with the increment of the producing time and fracture conductivity．Compared with the conventional models，calculation results achieved by this proposed model are in a better agreement with the measured data from an actual well．

Keywords：tight gas reservoir，fractured horizontal wells，point sink(congruence)function，principle of superposition．Non-uniform flow，unstable production calculation

準確預測致密氣藏壓裂水平井產量及分布對于壓裂水平井優化設計具有重要意義。有關壓裂水平井產能模型大致可分為兩類：一類是采用商用數值模擬軟件，對水平井壓裂形成多條裂縫的產量影響因素進行分析^[1-3]；另一類是根據源匯的思想，將壓裂水平井裂縫處理成點(線)匯，即首先利用疊加原理或積分變換，建立起多個點(線)匯同時生產時在裂縫尖端的壓力降落響應^[4-13]，然后將裂縫上的流動等效處理成微型平面徑向流^[4，7-13]或者平板流動模型^[14]，利用點(線)匯在裂縫面上參與地層和裂縫流動時的壓力相等建立起連續性方程進行求解。本文參考文獻[4-13]考慮沿裂縫面均勻產量的假設使數學上處理更方便，但是壓裂水平井在生產過程中裂縫井段存在干擾以及裂縫內流動時的摩阻壓降，使得上述假設與實際情況存在較大差異。為了解決上述問題，筆者采用空間和時間離散技術，基于瞬時源函數和疊加原理，考慮裂縫面上非均勻產量流入以及裂縫內流動變化情況，建立了氣藏壓裂水平井非穩態產量模型，并將計算結果與實例井以及傳統模型計算結果進行了對比，吻合程度高，驗證了模型的可靠性。

1　氣藏滲流模型

假設無限大上頂下底封閉氣藏中的1口壓裂水平井被垂直裂縫分成若干段，氣體只通過裂縫流入水平井筒。水平井半徑為rw，長度為L，井在油氣藏中心位置坐標為(x0，y1，z0)～(x0，y2，z0)，與y軸平行。氣藏均質各向同性，厚度為h、孔隙度為j、滲透率(K)為常數；第k條裂縫的單翼裂縫半長為xfk、裂縫寬度為wfk，考慮水平井筒為無限導流，氣藏初始壓力為常數pi。由于裂縫完全貫穿氣層，可將壓裂水平井的裂縫簡化成一線匯^[15]；將第k條裂縫單翼均分成ns個線匯單元(每段長為Dxfk＝xfk／ns)。每一個線匯單元的生產可處理為l口直井進行考慮。定井底流壓生產時，產量是不斷發生變化，將時間段取很小，可以近似認為在該段時間內產量為定值。無限大地層中一口直井以定產量生產時的不穩定滲流方程為^[16]：

 

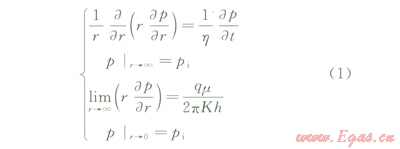
式中r為徑向距離，m；p為地層壓力，MPa；h為導壓系數，m²·MPa/(mPa·s)；h＝K/(mcj)；m為流體黏度，mPa·s；c為地層綜合壓縮系數，MPa^-1；t為生產時間，ks；pi為原始地層壓力，MPa；q為井產量，m³／ks；h為儲層厚度，m；K為巖石滲透率，D；j為孔隙度。

平面直角坐標系下，設在裂縫k上有一線匯M(x2fk,i，ykf)(產量為qfk,i)，在裂縫k+1上有一觀察點位于O(xfk+,j，yfk+1)，線匯qfk,i連續生產時間t后在O點產生的壓力降落為：

 

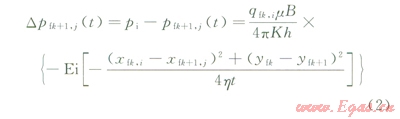
當裂縫k上存在ns個線匯單元時，可以得到第k條裂縫上ns個線匯單元同時生產時間t后在O點的產生壓力降落；類似的，也能得到N條裂縫上2N×ns個線匯同時生產時在O點的壓力降落為：

 

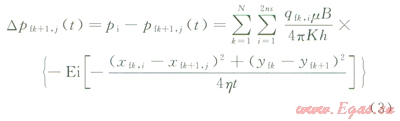
式(3)就是任意時刻所有裂縫線匯單元同時在O點產生壓力降落進行疊加后得到的儲層滲流方程，該方程考慮了壓裂水平井多條裂縫以及各裂縫線匯單元間的干擾作用。

當儲層流體為氣時，根據壓力函數的定義和真實氣體狀態方程，并將地下產量轉換成地面標準情況下的氣體產量^[4，10]，式(3)可寫為：

 

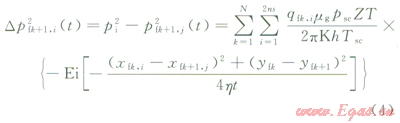
式中pfk+1,i為裂縫k+1上線匯單元j的裂縫壁處壓力，MPa；N為壓裂裂縫總條數；ns為裂縫單翼線匯單元數目；qfk+i為裂縫k上線匯單元i的產量，m³／ks；mg為氣體黏度，mPa·s；psc為氣體臨界壓力，MPa；Z為氣體偏差因子，無因次；T為儲層溫度，℃；Tsc為氣體臨界溫度，℃；(xfk,i，yfk)為裂縫k上線匯單元i的中心坐標；(xfk+1,j，yfk+1)為裂縫k+1上線匯單元j的中心坐標。

　　式(4)就是所有裂縫線匯單元同時生產時間t后在O點產生的壓力降落響應方程。

2　裂縫流動模型

假設流體經過裂縫面進入裂縫后向水平井筒的流動為一維線性流動(圖1)。為了便于計算，將微元段處理成矩形進行汁算，裂縫寬度為wfk+1，以計算流體在裂縫中流動時產生的壓力降落。

 

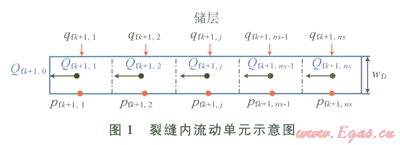
由達西定律計算第k+1條裂縫第j微兀段(點Ofk+1,j)流動到水平井筒(點Ofk+1,0)間壓差為：

 

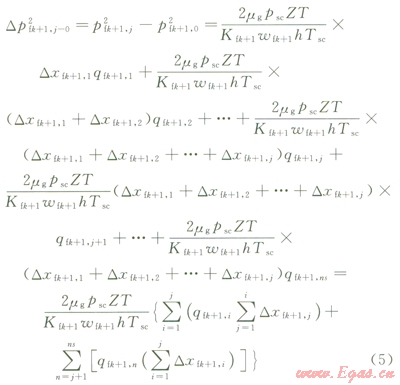
式中Dp²fk+1,j-0為裂縫k+1上線匯單元j在裂縫內流動時產生的壓差，MPa；Kfk+1為裂縫k+1的裂縫滲透率，mD；wfk+1為裂縫k+1的裂縫寬度，m。

式(5)中第一項表示第k+1條裂縫第j及之前線匯單元產量在裂縫內流動時產生的壓降；第二項表示第k+1條裂縫第j個之后線匯單元產量在裂縫內流動時產生的壓降。

3　耦合流動模型

氣體從儲層流到水平井筒的過程可以分為氣藏滲流和裂縫內流動兩個過程，式(4)、式(5)已經建立起了相應的壓降方程；考慮到氣體在儲層內流動和流體在裂縫內流動時在裂縫壁面處的壓力相等，將式(4)、(5)聯守可建市地層壓力為井底流壓的壓力連續方程；由于假設井筒無限導流，各裂縫在與水平井筒相交節點處O0的壓力相等，定井底流壓(pwf)生產時邊界條件為：

pfk+1,0＝pwf 　          　　   (6)

式中pwf為水平井筒井底流壓，MPa。

聯立方程(4)、(5)、(6)整理可得到第是+1裂縫第j個線匯的儲層裂縫耦合流動方程：

 

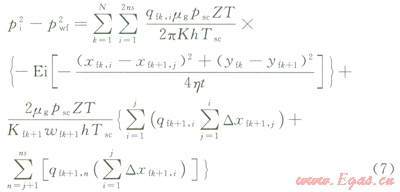
式(7)中變量為每一個線匯產量，這樣就建立起了壓裂水平井裂縫與氣藏耦合的瞬態滲流數學模型。

對于一口壓裂N條橫向裂縫的壓裂水平井，可以求解下面的方程組計算任意時刻的各裂縫線匯的產量qf1，1，qf1，2，…，qf1，ns，q21，1，qf2，2，…，qfN，2ns即

 

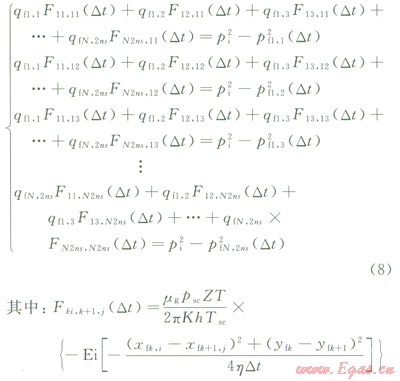
由于考慮氣體只通過裂縫流入到水平井筒，所以氣井總產量為：

 

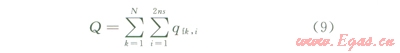
如果井底壓力(pwf)已知，聯立方程式(5)、(8)便可求得每個線匯的產量，根據式(9)就可求得總產量。

上面就完成了第一個Dt時間步長下各線匯單元及總產量計算；對于各線匯單元而言，由于產量會隨生產時間發生變化，這樣就需要利用時間疊加來求得任意時刻的值。設時間段步長為Dt，當時t＝mDt(第m個時間段的結尾)，則對第k+1條裂縫的第j個線匯，可得到：

 

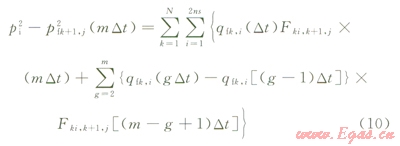
與第一個時間步長下的產量計算一樣，根據井底壓力約束和總產量約束，組成封閉方程組求解，從第一個時間步長開始，循環求解，直到得到第m個時間步長的結果。

4　計算實例及敏感性分析

4.1　模型的驗證

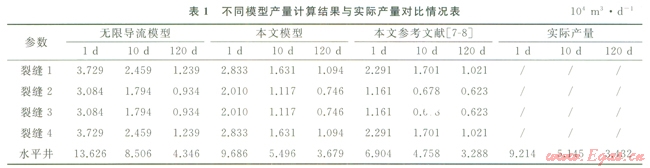
某致密氣藏水平井埋藏深度2600 m，水平段長度為600m，有效厚度為l5.5，孔隙度為12.0％，滲透率為0.75mD，氣層溫度為68℃，氣體黏度為0.035mPa·s，氣體偏差因子為0.89，原始地層壓力30MPa，井底流壓22MPa。壓裂形成4條等間距裂縫，裂縫長度100m，裂縫導流能力30D·cm。

分別按照裂縫無限導流模型、本文模型以及本文參考文獻[7-8]的計算結果與實際產量對比(表1)。可以看出，本文模型的計算結果從初期到穩定生產階段最接近，表明本文模型準確性高。從3種模型計算結果的對比來看：無限導流模型計算生產ld時的產量為13.626×10⁴m³／d、生產120d后產量為4.346×10⁴m³／a，遠高于實際產量，表明不能忽略裂縫內壓力損失的影響。從本文參考文獻[7-8]模型的計算結果與實際產量對比可以看出，生產初期差別較大(分別為6.904×10⁴m³／a和9.214×10⁴m³／d)，而在生產120d的差別變小，這表明采用均勻產量分布的假設與實際情況存在較大偏差。

 

4.2　裂縫產量分布與位置的關系

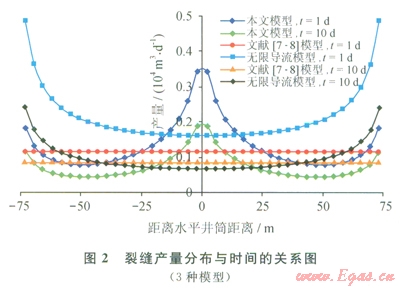
圖2是3種模型第l條裂縫的產量分布對比結果。采用無限導流模型計算結果表明，由于沒有考慮裂縫內的壓力降落，在生產初期(t＝ld)裂縫內的產量分布為“U”形，裂縫兩端產量相對較高，這與本文參考文獻[15]規律一致；本文模型考慮了裂縫產量非均勻分布以及裂縫內的壓力損失，裂縫產量在水平井筒附近出現局部峰值，且隨裂縫內壓力損失增大，井筒附近裂縫產量的峰值越明顯，這是由于越靠近井簡裂縫生產壓差越大，裂縫產量越高造成的；由于裂縫段內相互干擾，隨著生產時間的增加，裂縫產量分布趨于均勻，但由于水平井筒壓力最低，裂縫上產量分布為近似“雙U”型，這與本文參考文獻[l4]規律相符合。

 

4.3　裂縫產量分布與時間的關系

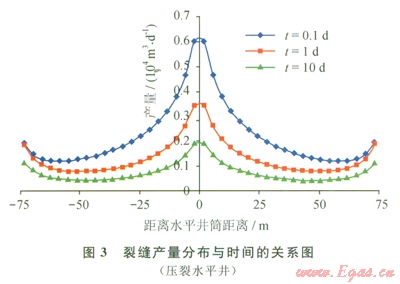
圖3是壓裂水平井第1條裂縫的產量分布與時間的關系曲線。由于裂縫為有限導流，氣體在裂縫內流動存在壓力差，生產初期(t＝0.1d)水平井井筒附近產量較高，裂縫遠端產量較低；隨時間增加(t＝10d)，壓力傳遞到裂縫遠端以及水平井筒附近裂縫段受到的干擾最為明顯，水平井筒附近的產量急劇減小，裂縫遠端產量略有減小；當生產時間大于100d時，整個系統的流動達到擬穩態階段，裂縫內產量分布趨于穩定。

 

4.4　裂縫產量分布與裂縫導流能力的關系

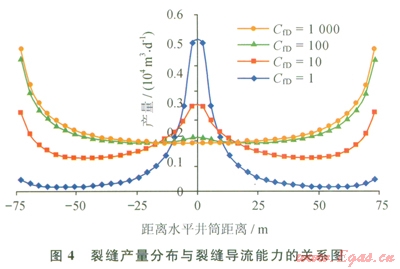
圖4是壓裂水平井擬穩態生產階段(t＝100d)第1條裂縫產量分布與裂縫導流能力的關系曲線。可以看出：裂縫導流能力越小，裂縫內產量分布越不均勻，水平井筒附近裂縫產量越高；當無因次裂縫導流能力大于l00時，裂縫產量分布均勻，趨近于無限導流裂縫內的產量分布。從無因次裂縫導流能力對產量的影響可以看出，裂縫導流能力越大，壓裂水平井產量越高，但隨著裂縫導流能力的增加，產量增幅逐漸變小。主要原因是當縫導流能力過低時，而氣層供給能力比較強，使得在裂縫附近流體聚集，產牛附加阻力，這時通過增加裂縫導流能力解除這部分附加阻力，就能確保產量明顯上升；但當縫裂縫導流能力過高時，而氣層供給跟不上，出現“抽空”現象，表現為導流能力的增加，產量增幅減小。因此，需要優化壓裂縫的導流能力，使得裂縫導流能力與儲層供給能力相一致，才能獲得最佳增產效果。

 

5　結論

1)基于瞬時點源函數和疊加原理，采用空間和時間離散技術，考慮裂縫面上的非均勻流入以及縫內摩阻變化，建立了致密氣藏壓裂水平井非穩態產量計算模型，該模型解決了定量預測壓裂水平井及裂縫上產量分布的定量預測。該模型與實際井產量及傳統模型的計算結果對比驗證了其可靠性。

2)壓裂水平井產量計算過程中，無限導流裂縫模型會導致計算產量遠高于實際產量，裂縫均勻產量的假設使得計算結果低于實際產量。

3)由于裂縫干擾，水平井筒兩端裂縫的產量高于中間裂縫的產量；由于裂縫非均勻流入以及裂縫內摩阻損失，裂縫產量在水平井筒附近出現局部峰值。

4)裂縫內產量分布受生產時間和裂縫導流能力的影響，流動時間越長，裂縫導流能力越大，裂縫內的產量分布越均勻。

 

參考文獻

[1]周竹眉，郎兆新．水平井油藏數值模擬的有限元方法[J]．水動力學研究與進展：A輯，l996，11(3)：261-270．

ZHOU Zhumei，LANG Zhaoxin．A finite element method for horizontal well reservoir simulation[J]．Journal of Hydrodynamic：Series A，1996，11(3)：261-270．

[2]張學文，方宏長，裘亦楠，等．低滲透油藏壓裂水平井產能影響因素[J]．石油學報，l999，20(4)：51-54．

ZHANG Xuewen，FANG Hongchang，QIU Yinan，et al．A study on factors affecting the performance of hydraulically fractured horizontal well in low permeability reservoirs[J]．Acta Petrolei Sinica，1999，20(4)：51-54．

[3]尹洪軍，呂杭，蔡明，等．非均質氣藏水平井三維滲流的產能預測方法[J]．數學的實踐與認識，2011，41(16)：59-64．

YIN Hongjun，LYU Hang，CAI Ming，et al．Productivity prediction method of 3D seepage horizontal wells in heterogeneity gas reservoir[J]．Mathematics in Practice and Theory，20ll，4l(16)：59-64．

[4]寧正福，韓樹剛，程林松，等．低滲透油氣藏壓裂水平井產能計算方法[J]．石油學報，2002，23(2)：68-71．

NING Zhengfu，HAN Shugang，CHENG Linsong，et al．Productivity calculation method of fractured horizontal wells in low permeability oil or gas field[J]．Acta Petrolei Sinica，2002，23(2)：68-71．

[5]AISSA Zerzar，YOUCEF Bettam．Interpretation of multiple hydraulically fractured horizontal wells in closed systems[C]//paper 84888-MS presented at the SPE In*ernational Improved Oil Recovery Conference in Asia Pacific．20-21 October 2003．Kuala Lumpur，Malaysia．New York：SPE，2003．

[6]BRANIMIR Cvetkovic，GOTSKALK Halvorsen，JAN sagen，et al．Modelling the productivity of a multifractured-horizontal well[C]//paper 71076-MS presented at the SPE Rocky Mountain Petroleum Technology Conference，21-23 May 2001，Keystone，Colorado，USA．New York：SPE，2001．

[7]曾凡輝，郭建春，何頌根，等．致密砂巖氣藏壓裂水平井裂縫參數的優化[J]．天然氣工業，2012，32(11)：54-58．

ZENG Fanhui，Gldo Jianchun，HE Songgen，et al．Optimization of fracture parameters of fractured horizontal wells in tight sandstone gas reservoirs[J]．Natural Gas Industry，2012，32(11)：54-58．

[8]徐嚴波，齊桃，楊鳳波，等．壓裂后水平井產能預測新模型[J]．石油學報，2006，27(1)：89-96．

XU Yanbp，QI Tao，YANG Fengbo，et al．New model for productivity test of horizontal well after hydraulic fracturing[J]．Acta Petrolei Sinica，2006，27(1)：89-96．

[9]張小濤，吳建發，馮曦，等．頁巖氣藏水平井分段壓裂滲流特征數值模擬[J]．天然氣工業，2013，33(3)：47-52．

ZHANG xiaotao，WU Jianfa，FENG Xi，et al．Numerical simulation of seepage flow characteristics of multi stage fracturing(MSF)in horizontal shale gas wells[J]．Natural Gas Industry，2013，33(3)：47-52．

[10]廉培慶，程林松，何理鵬，等．氣藏壓裂水平井非穩態流動分析[J]．計算力學學報，2011，28(4)：579-583．

LIAN Peiqing．CHENG Linsong,HE Lipeng，et al．Analysis of transient flowing model for fractured horizontal well in gas reservoir[J]．Chinese Journal of Computational Mechanics，2011，28(4)：579-583．

[11]孫海，姚軍，廉培慶，等．考慮基巖向井筒供液的壓裂水平井非穩態模型[J]．石油學報，2012，33(1)：117-122．

SUN Hai，YAO Jun，LIAN Peiqing，et al．A transient reservoir／wellbore coupling model for fractured horizontal wells with consideration of fluid inflow from base rocks into wellbores[J]．Acta Petrolei Sinica，2012，33(1)：117-122．

[12]郝明強，胡永樂，李凡華．特低滲透油藏壓裂水平井產量遞減規律[J]．石油學報，2012，33(2)：269-273．

HAO Mingqiang，HU Yongle，LI Fanhua．Production decline laws of fractured horizontal wells in ultra-low permeability reservoirs[J]．Acta Petrolei Sinica，2012，33(2)：269-273．

[13]王志平，朱維耀，岳明，等．低、特低滲透油藏壓裂水平井產能計算方法[J]．北京科技大學學報，2012，34(7)：750-754．

WANG Zhiping，ZHU Weiyao，YUE Ming，et al．Amethod to predict the production of fractured horizontal wells in low／ultra low permeability reservoirs[J]．Journal of University of Science and Technology Beijing，2012，34(7)：750-754．

[14]汪志明，齊振林，魏建光，等．裂縫參數對壓裂水平井入流動態的影響[J]．中國石油大學學報：自然科學版，2010，34(1)：73-78．

WANG Zhiming，QI Zhenlin，WEI Jianguang，et al．Influence of fracture paranleters on inflow performance of fractured horizontal wells[J]．Journal of China University of Petroleum：Edition of Natural Science，2010，34(1)：73-78．

[15]李軍詩．壓裂水平井動態分析研究[D]．北京：中國地質大學，2005．

LI Junshi．A Study of performance analysis of horizontal wells with a single or muhiple fractures[D]．Beijing：China University of Geosciences，2005．

[16]李傳亮．油藏工程原理[M]．北京：石油工業出版社，2011．

LI Chuanliang．Reservoir engineering principles[M]．Beijing：Petroleum Industry Press，2011．

 

本文作者：曾凡輝  王樹義  郭建春  江啟峰  張楠喬

作者單位：“油氣藏地質及開發工程”國家重點實驗窒·西南石油大學

  中國石油華北油田公司第二采油廠

  “流體及動力機械”教育部重點實驗室·西華大學