摘 要

摘　要：針對某帶蓄冷裝置的區域供冷系統，基于時間序列對負荷進行預測。以制冷機組日運行成本最小化為目標，建立能源站優化控制模型，分析了50％、75％、l00％設計冷負荷條件下的優化控

摘　要：針對某帶蓄冷裝置的區域供冷系統，基于時間序列對負荷進行預測。以制冷機組日運行成本最小化為目標，建立能源站優化控制模型，分析了50％、75％、l00％設計冷負荷條件下的優化控制策略。

關鍵詞：區域供冷  蓄冷裝置  時間序列  負荷預測  優化控制

Load Prediction and Optimal Control of District Cooling System with Cold Storage Device

Abstract：The load of a district cooling system with cold storage device is predicted based on time sequence．Taking the minimum operation cost as the objective，the optimal control model of energy station is set up．The optimal control strategies under the design cold load conditions of 50％,75％ and l00％are analyzed．

Key words：district cooling j cold storage device；time sequence；load prediction；optimal control

1　項目概況

區域供冷系統可配置高效、環保的大型設備，通過專業化的管理實現供能的產業化^[1-3]。更重要的是可利用蓄冷技術降低機組的裝機容量，緩解電力供應緊張形勢及電力建設與新增用電的矛盾。對于帶蓄冷裝置的區域供冷系統，核心問題是能源站的優化控制，即合理安排和分配峰谷電價時段內制冷機組制冰冷量、供冷量及蓄冰槽融冰供冷量，使能源站能夠更加經濟地滿足負荷需求。學術界及工程界普遍認為，負荷預測為能源站優化控制提供了基礎^[4-5]。本文以天津文化中心南區的區域供冷系統(帶蓄冷裝置)能源站作為研究對象，對負荷預測方法及能源站優化控制策略進行探討。

天津文化中心南區能源站供冷對象為博物館、美術館、圖書館、大劇院等單體公共建筑，總供冷面積為304336m²，設計冷負荷為26866kW。采用地埋管地源熱泵，地埋管換熱器埋設于景觀湖底。能源站配置2臺制冷能力為l344kW的螺桿式熱泵機組作為基載機，4臺制冷能力為3573kW的離心式三工況(制冰、供冷、供熱工況)熱泵機組作為主機，蓄冰槽的蓄冷能力為260.6GJ。

2　基于時間序列的動態負荷預測

基于時間序列的動態預測是一種以時間為參數的離散隨機過程，針對平穩時間序列，前人已經建立了諸多成熟的預測模型。其中，具有代表性的是由Box和Jenkins提出的差分自回歸移動平均模型(ARIMA)。該模型的基本思路是：對于非平穩時間序列，用若干次差分使其成為平穩時間序列，再用自回歸滑動平均模型(ARMA)對平穩時間序列建模，最后經反變換得到非平穩時間序列的動態預測模型^[6]。

本文選擇以小時為單位，在選定的時間間隔基礎上，對負荷數據進行分析與處理。雖然以24h為周期的負荷數據呈現周期變化趨勢，但仍為非平穩時間序列，因此必須采用差分方法進行平穩化處理，平穩化處理后再進行ARMA模型的建立^[7]。

在差分自回歸移動平均模型的基礎上，考慮預測誤差，對初步預測結果進行修正，從而得到最終預測結果。預測誤差算法：從歷史時間序列中選取一定量的觀測時間序列，采用一次簡單移動平均算法計算預測誤差。對于觀測時間序列蜀，Xq，Xq-1，…，Xq-N+1預測誤差d的計算式為：

 

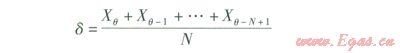
式中d——預測誤差

Xq、Xq-1、…、Xq-N+1——q時刻、q-1時刻、q-N+1時刻的觀測時間序列

N——觀測時間序列的數量

經過修正的t時刻最終預測結果Ft,f的計算式為：

Ft,f＝d+Ft,p

式中Ft,f——經過修正的t時刻最終預測結果

Ft,p——t時刻初步預測結果

3　能源站優化控制模型

3.1　蓄水槽模型

蓄冰槽雖然不是能耗設備，但由于其傳熱性能決定了蓄冷、釋冷速率，將影響能源站的優化控制。引入狀態變量x表示蓄冰槽的剩余冷量比例；引入控制變量u表示蓄冰槽工作狀態的速率，蓄冰槽工作狀態分為蓄冷、釋冷、不蓄冷也不釋冷，蓄冷時u取正值，釋冷時“取負值，不蓄冷也不釋冷時u為0。蓄冰槽模型可表達為：

xk+1＝xk+ukDt

xmin≤xk≤xmax

umin≤uk≤umax

式中xk+1——第k+1小時的蓄冰槽剩余冷量比例

xk——第k小時的蓄冰槽剩余冷量比例

uk——第k小時蓄冰槽工作狀態速率，h^-1

Dt——時間間隔，h

xmin——蓄冰槽最小剩余冷量比例

xmax——蓄冰槽最大蓄冷量比例

umin——最大釋冷速率，h^-1

umax——最大蓄冷速率，h^-1

3.2　優化控制目標

忽略蓄冰槽的熱損失，將制冷機組的制冰冷量與蓄冰槽的融冰供冷量視為相等。設能源站每日供冷時間為0小時，第k小時的冷負荷為Fk。其中制冷機組承擔的供冷量為Fc,k，運行成本為Fc,k；蓄冰槽承擔的融冰供冷量為FL,k，運行成本(即制冷機組的制冰成本)為FL,k。則制冷機組的日運行成本Fee的計算式為：

 

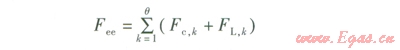
式中Fee——制冷機組日運行成本，元

q——日供冷時間，h

Fc,k——第k小時制冷機組的供冷成本，元

FL,k——第k小時蓄冰槽融冰供冷成本（即制冷機組的制冰成本），元

將制冷機組最小日運行成本Fee,min作為優化控制目標：

 

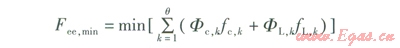
式中Fee,min——制冷機組最小日運行成本，元

Fc,k——第k小時制冷機組供冷量，kW

¦c,k——第k小時制冷機組單位供冷量成本，元/kW

FL,k——第k小時蓄冰槽融冰供冷量(即制冷機組制冰冷量)，kW

¦L,k——第k小時蓄冷槽單位融冰供冷量成本(即制冷機組單位制冰冷量成本)，元／kW

供冷工況下第k小時制冷機組部分負荷率hc,k的計算式為：

 

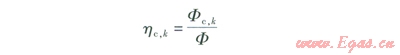
式中hc,k——供冷工況下第k小時制冷機組部分負荷率

F——制冷機組的制冷能力，kW

制冰工況下第k小時制冷機組部分負荷率叩hL,k的計算式為：

 

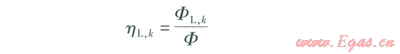
式中hL,k——制冰工況下第k小時制冷機組部分負荷率

供冷工況下第k小時制冷機組電功率Pc,k的計算式為：

Pc,k＝P(d+ehc,k+gh²c,k)

式中Pc,k——供冷工況下第k小時制冷機組電功率，Kw

P——制冷機組的額定電功率，kW

d、e、g——系數，由制冷機組性能曲線擬合得到

供冷工況下第k小時制冷機組單位供冷量成本¦c,k的計算式為：

¦c,k＝chP(d+ehc,k+ gh²c,k)

式中ch——電力高峰時段單位發電功率費用，元/kW

同理，制冰工況下第k小時制冷機組單位制冰冷量成本¦L,k的計算式為：

¦L,k＝cLP(d+ehL,k+ gh²L,k)

式中cL——電力低谷時段單位發電機功率費用，元/kW

3.3　約束條件

無論供冷工況還是制冰工況，制冷機組的制冷量都不能超過制冷能力。制冷機組供冷量與蓄冰槽融冰供冷量之和應滿足冷負荷要求。能源站為用戶正常供冷時間為8：00—22：00，其他時間的值班負荷為800 kW。

4　優化控制結果

50％、70％、l00％設計冷負荷時的運行策略分別見圖1～3。

 

 

 

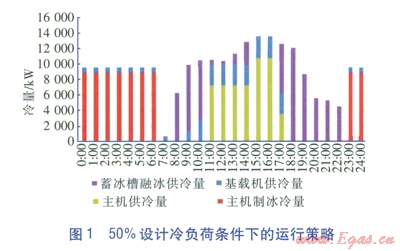
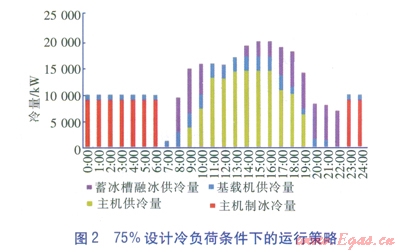
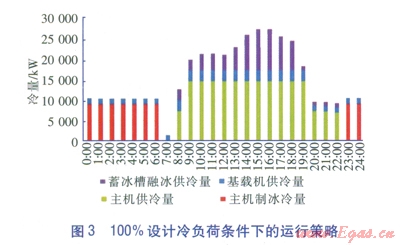
由圖l～3可知，在低谷電價時段，充分利用制冷主機進行制冰；在峰段電價時段，充分利用融冰制冷，減少高峰電力的使用。由此可知，根據能源站優化控制模型制定的控制策略，可獲得較好的經濟效益。

 

參考文獻：

[1]康英姿，華賁．區域供冷系統與燃氣分布式能源系統的結合[J]．煤氣與熱力，2007，27(2)：62-66．

[2]張朝輝，李震，端木琳．區域供冷技術的應用與技術條件[J]．煤氣與熱力，2007，27(3)：86-89．

[3]康英姿，華賁．區域供冷系統的技術與經濟性分析[J]．煤氣與熱力，2007，27(11)：79-82．

[4]孫靖，程大章．基于逐時空調負荷預測的冰蓄冷優化控制策略[J]．智能建筑與城市信息，2005(5)：24-29．

[5]倪雪梅，辜興軍，許志浩．冰蓄冷系統優化蓄冷的策略的探討[J]．制冷與空調，2004(1)：21-24．

[6]STETHIRNANN D H．Optimal control for cool storage[J]．ASHRAE Trans．，l989(1)：1-5．

[7]KAWASHIMA M．Hourly thermal load prediction for the next 24 hours by ARIMA，EWMA，LR and an artificial neural network[J]．ASHRAE Trans．，l995(1)：186-200．

 

本文作者：殷洪亮  由玉文  翟文鵬  郭春梅  梁春峰

作者單位：天津城建大學能源與安全工程學院

  中國民航大學