摘要：介紹支持向量機的原理和支持向量回歸模型，提出支持向量回歸(SVR)模型的城市燃氣短期負荷預測方法。探討輸入樣本數據的選擇和預處理方法、核函數和支持向量機參數的選擇，結合某城市燃氣日負荷數據進行燃氣短期負荷預測。與BP神經網絡預測方法相比，支持向量回歸模型預測方法用于小樣本情況下的燃氣短期負荷預測精度略高。

關鍵詞：燃氣負荷預測；  短期負荷；  支持向量機；  BP神經網絡；  支持向量回歸模型

Short-term Gas Load Forecast Based on Support Vector Machine

Abstract: The principle of support vector machine and the support vector regression model are introduced. A short-term city gas load forecast method based on support vector regression model is proposed. The selection and pretreatment method of input sample data and the selection of kernel function support vector machine parameters are discussed. The short-term gas load forecast is conducted with the daily gas load data of a city. For small sample data，the forecast method based on support vector regression model has higher short-term city gas load forecast precision than the forecast method based on BP neural network.

Key words: gas load forecast；short-term load； support vector machine；BP neural network；support vector regression model

1 概述

國內外對燃氣負荷預測的研究^[1-7]主要開始于20世紀后期，隨著技術進步和計算機的廣泛應用，各種新理論和方法相繼被應用于燃氣負荷預測。早期常用的方法是基于統計學的回歸分析和時間序列分析，但是由于負荷預測問題的高度非線性和不確定性，傳統方法往往難以建立精確的數學模型，為解決這一問題，我們引入了灰色理論、人工神經網絡和支持向量機等理論方法。本文利用支持向量回歸模型進行燃氣短期負荷預測研究，為建立城鎮燃氣短期負荷預測模型提供一條新途徑。

2 支持向量機的原理和支持向量回歸模型

支持向量機(Support Vector Machine)簡稱SVM^[8]，是一種監督式學習的方法，廣泛應用于統計分類以及回歸分析中，其算法見圖1。支持向量機首先通過內積核函數K(X)定義的非線性變換將輸入空間X變換到一個高維空間，然后在這個空間中求最優分類面，其輸出Y是中間節點的線性組合，每個中間節點對應一個輸入樣本與一個支持向量的內積，因此也被稱為支持向量網絡。研究表明^[9-10]，相對于神經網絡而言，支持向量回歸模型不存在局部極小值問題，對于解決模糊、隨機、不確定性、樣本數有限和非線性的復雜問題具有明顯優勢。支持向量機從結構風險最小化原則出發，為機器學習提供了一個嶄新的方法，被認為是小樣本學習中一種很好的機器學習算法。

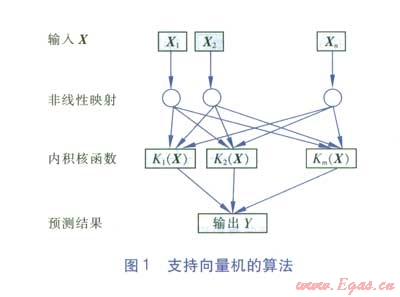
SVM常用的學習算法有Chunking算法、分解算法、序列最小優化SM0法、最近點快速迭代(NPA)算法和最小二乘法等。SVM方法在建模過程中，核函數及其參數對模型預測的執行效率和推廣預測能力影響較大，對于SVM參數的優化選取，目前尚未有統一的最佳方案，常用的方法就是使參數在一定范圍內取值，采用試算方法來選取最優的一組參數。為避免試算的盲目性，除常規的網格劃分方法外，目前常用的啟發式參數尋優方法還有遺傳算法(GA)和粒子群優化算法(PSO)等。  

2.1 基本原理

假設樣本(x_i，y_i)，i=1，…，n，x_i∈Rⁿ，y_i∈R(Rⁿ為n維的實數空間，R為實數)，支持向量機的基本原理就是將學習樣本(x_i，y_i)通過映射函數ø映射到一個高維特征空間，然后選擇適當的核函數K(X)和懲罰參數C，通過求解二次優化問題可得到松弛變量δ_i和參數b。

優化的目標函數為F=w^Tw，目標函數F可以保證分類的最優性，約束條件(式2)則保證分類的正確性。為了消除異常樣本的影響，引入松弛變量δ_i，相應的目標函數可以表示為：

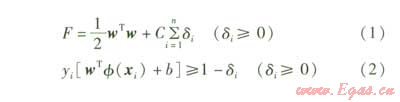
式中 w——超平面的權值向量

     C——懲罰參數，對錯誤分類起懲罰作用

    δ_i——松弛變量，其作用是衡量對樣本(x_i，y_i)的誤分類程度

     b——參數

向量x_i通過函數ø (x)被映射到高維空間，K(x_i，y_i)=ø(x_i^T)ø(x_j)為核函數。支持向量機通過將輸入空間映射到一個高維內積空間，解一個線性約束的二次規劃問題得到全局最優解，從而有效避免了“維數災難”，保證了收斂速度。在最優分類面中選擇適當的核函數，可以實現某一非線性變換后的線性分類，且不增加其計算的復雜性。

在SVM中最常用的幾種核函數見式(3)～(6)，其中線性核函數可以看作是多項式核函數的一種特殊情況。

2.2支持向量回歸模型(SVR)

1996年國外相關學者提出了一種利用支持向量機進行回歸的計算方法。該方法需要解決的問題與式(1)類似，通常被稱為支持向量回歸(SVR)模型。假設待回歸的函數為f(x)=wx+P，樣本數據(x_i，y_i)，i=1，…，n，x_i∈Rⁿ，y_i∈R，按照支持向量機理論，其擬合函數為：

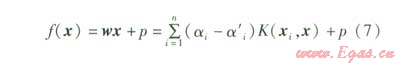
式中 α_i,α＇_i,p——參數

式(7)中的參數α_i,α＇_i,p通過解下面的二次優化問題獲得，優化的目標函數為：

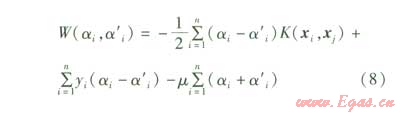
約束條件為：

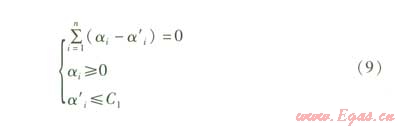
式中 μ——預測誤差

     C₁——懲罰因子，表示對超出誤差μ的樣本的懲罰程度

3 燃氣負荷預測的支持向量回歸模型

燃氣負荷是由數量眾多的各類用戶用氣所形成，由于影響負荷的各種自然、社會和經濟條件不斷變化，以及終端用戶的使用情況影響，導致燃氣負荷處于一個動態的變化過程。燃氣負荷具有時變性，對于短期負荷預測而言，最重要的影響因素是星期幾、溫度、天氣、是否節假日等特殊日等。

假設已有多日的燃氣負荷實際數據(x_i，y_i)，i=1，2，…，m，其中x_i為第i天燃氣負荷的影響因素，y_i為第i天的燃氣負荷實測值。利用支持向量回歸模型進行燃氣負荷預測，即建立每天燃氣負荷影響因素x_i與燃氣負荷y_i之間的非線性函數關系，即：

根據支持向理機理論，該非線性函數關系可以用支持向量機對前i-1天實測數據的學習來獲得，其回歸計算公式為：

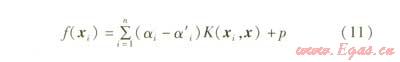
3.1 確定輸入輸出

燃氣負荷預測支持向量回歸模型的輸入因素通常為溫度(包括最高、最低和平均溫度)、日期和天氣情況，輸出值則為當日的燃氣負荷。支持向量回歸模型只能處理非模糊的定量數據，采用較多的負荷相關因素作為輸入可以提高預測的精度，輸入的影響因素越多，網絡運算的精度越高，樣本訓練所需的時間也會越多，因此在實際應用時應根據已有資料選擇適當數量的輸入因素。

燃氣負荷處于一個隨機非平穩的過程，由于受到各種因素的影響，其歷史數據常常包含部分不良數據，因此通常在使用前要進行預處理，例如采用低通濾波法去除分散或連續出現的不大的尖峰擾動，使樣本數據更具有實際意義。在樣本選擇和優化處理過程中，如果數據源中有大量未經處理或者虛假的數據，將會妨礙對網絡的正確訓練，因此剔除或使用正常數據置換那些不符合實際的異常樣本數據，確定出數據的合適數目。

3.2 參數的優選

支持向量機參數的優選主要包括兩部分內容，一是核函數的選擇，二是參數的優選。通常情況下，我們優先選擇RBF核函數，與其他核函數相比，它在數值計算上具有一定優勢，而線性核函數和Sigmoid核函數如果選擇適合的參數都可以轉變為RBF核函數。對于支持向量機參數的優選，目前最常用的方法是采用網格劃分與交叉檢驗相結合的方法。

4 預測實例

4.1 預測流程

利用支持向量機進行燃氣短期負荷預測的基本流程見圖2。

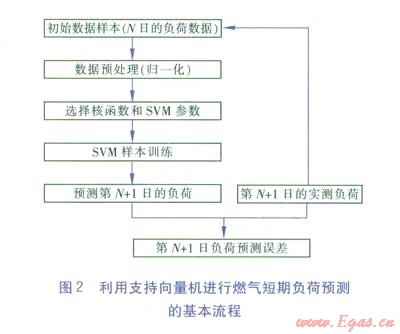
4.2 預測實例

選擇某城市21天的燃氣負荷數據，初始訓練樣本為前7天的負荷數據(見表l)，利用SVR預測第8天的燃氣負荷，然后將第8天的實測負荷并入初始訓練樣本，再利用SVR預測第9天的燃氣負荷，以此類推，可以得到第8天至第21天的燃氣負荷預測值及相對誤差(見表2)。

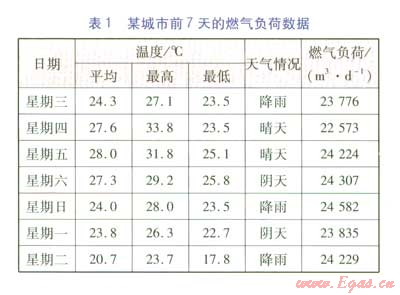
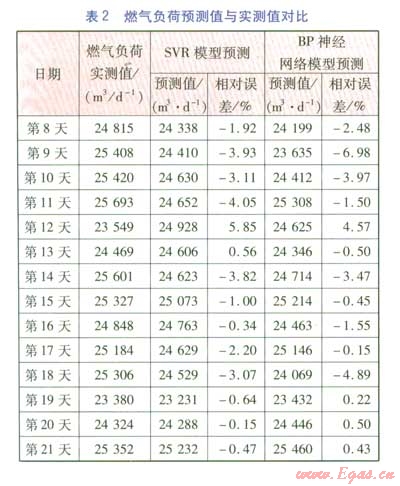
以星期幾、平均溫度、最高溫度、最低溫度、天氣情況作為SVR模型的輸入參數，模型輸出為當日的燃氣負荷。由于各影響因素差別較大，為方便支持向量機的訓練和學習，需要將學習樣本和預測樣本數據進行歸一化處理，通常將樣本數據調整為[0，1]或[-1，1]，分別用支持向量回歸模型和BP神經網絡模型進行訓練和預測，數據對比見表2。其中支持向量回歸模型選擇RBF函數作為核函數，參數的選擇采用網格劃分和交叉檢驗來確定；BP神經網絡包括1個隱含層，根據試算結果選擇9個節點。

由表2可以看出，對于燃氣短期負荷的預測，SVR模型和BP神經網絡模型預測這兩種預測方法，除個別點外，相對誤差基本都在5％以內，預測值與實測值吻合良好。樣本數量較少時，SVR模型預測方法較BP神經網絡模型預測精度更高，隨著樣本數量的增大，兩者的預測相對誤差都呈下降趨勢。綜上所述，利用SVR模型預測燃氣短期負荷可行，并且對于小樣本數據，其預測準確度略高于BP神經網絡模型預測。

5 結論

燃氣短期負荷與其影響因素之間的關系是復雜的非線性關系，用傳統的數學模型很難處理。本文將支持向量機應用于城市燃氣短期負荷預測，建立星期幾、平均溫度、最高溫度、最低溫度、天氣情況與燃氣負荷的支持向量回歸模型，對某城市燃氣負荷進行預測，與BP神經網絡的預測結果對比后顯示，SVR預測方法準確度略高，具有很高的實用價值，并且在解決小樣本、非線性及高維模式識別問題中具有特有的優勢。

參考文獻：

[1] 楊愛萍，鄧連杰，劉鳳國.城市燃氣負荷預測技術應用分析[J].煤氣與熱力，2011，31(9)：A39-A41.

[2] 焦文玲，金佳賓，廉樂明，等.時間序列分析在城市天然氣短期負荷預測中的應用[J].哈爾濱建筑大學學報，2001，34(4)：79-83.

[3] 焦文玲，朱寶成，馮玉剛.基于BP神經網絡城市燃氣短期負荷預測[J].煤氣與熱力，2006，26(12)：12-15.

[4] 劉燕，張應輝，杜學平.基于同歸分析的北京市天然氣供應規模預測[J].煤氣與熱力，2010，30(6)：A26-A29.

[5] 嚴銘卿，廉樂明，焦文玲，等.燃氣負荷及其預測模型[J].煤氣與熱力，2003，23(5)：259-262.

[6] 焦文玲，鄒濤，鞏曉峰，等.燃氣日負荷影響因素的相關分析和偏相關分析[J].煤氣與熱力，2010，30(5)：Bol-1705.

[7] 姚健，周偉國，張中秀.人工神經網絡法燃氣日負荷預測輸入變量選取[J].煤氣與熱力，2010，30(1)：A28-A30.

[8] 浦星材，沈曉風，張清揚，等.基于偏最小二乘法的支持向量機短期負荷預測[J].電網與清潔能源，2011，27(10)：32-35.

[9] 馬文濤.參數優化LSSVM的巷道圍巖松動圈預測研究[J].巖土力學，2007，28(s1)：460-464.

[10] 趙洪波.支持向量機在隧道圍巖變形預測中的應用[J].巖石力學與工程學報，2005，24(4)：649-652.

本文作者：郭微 姜德義

作者單位：重慶大學煤礦災害動力學與控制國家重點實驗室